APPLY VECTOR (CROSS) PRODUCT OF TWO VECTORS

 Understanding the Cross Product

The cross product accumulates interactions between different dimensions. Taking two vectors, we can write every combination of components in a grid:

This completed grid is the outer product, which can be separated into the:

Dot product, the interactions between similar dimensions (x*x y*y, z*z)
Cross product, the interactions between different dimensions (x*y,y*z, z*x, etc.)

Defining the Cross Product

The dot product represents vector similarity with a single number:

(Remember that trig functions are percentages.) Should the cross product (difference between interacting vectors) be a single number too?

Let’s try. Sine is the percentage difference, so we could use:

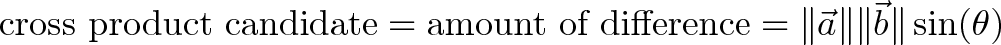
Unfortunately, we’re missing a lot of detail. x is 100% different from both y and z, but shouldn’t x*y and x*z be different from each other? As Tolstoy wrote, “All happy families are alike; each unhappy family is unhappy in its own way.”

Instead, let’s express these unique differences as a vector:

• The size of the cross product is the numeric “amount of difference” (with sin(theta) as the percentage)
• The direction of the cross product is based on both inputs: it’s the direction orthogonal to both (i.e., favoring neither)

A vector result represents the x*y and x*z separately, even though y and z are both “100% different” from x.

(Should the dot product be turned into a vector too? Well, we have the inputs and a similarity percentage. There’s no new direction that isn’t available from either input.)

Properties of the Cross Product:

• The length of the cross product of two vectors is 
• The length of the cross product of two vectors is equal to the area of the parallelogram determined by the two vectors (see figure below).
• Anticommutativity:
• Multiplication by scalars: 
• Distributivity: 
• The scalar triple product of the vectors a, b, and c: 
• The volume of the parallelepiped determined by the vectors a, b, and c is the magnitude of their scalar triple product.
• The vector triple product of the vectors a, b, and c: 

Note that the result for the length of the cross product leads directly to the fact that two vectors are parallel if and only if their cross product is the zero vector. This is true since two vectors are parallel if and only if the angle between them is 0 degrees (or 180 degrees).

Example

To find the area of the triangle with vertices (1,1,3), (4,-1,1), and (0,1,8), one could find the length of one of the altitudes of the triangle and proceed to find A=1/2(altitude)(base). However, this may not be an easy task in three dimensions. So consider finding the one-half the area of the parallelogram determined by the vector a from (1,1,3) to (4,-1,1) and the vector b from (1,1,3) to (0,1,8). Then a=<2-1,2-(-1),2-3>=<3,-2,-2> and b=<-1,0,5>. Using the result from the previous example and property number two above, we have the length of the cross product (and therefore the parallelogram determined by a and b) as

So, the area of the traingle is one-half this quantity, or 8.26.
The cross product occurs in many formulas in physics. Some examples include the curl of a vector field (see also Stoke's Theorem), torque, and many integrals over surfaces.

Calculating The Cross Product

A single vector can be decomposed into its 3 orthogonal parts:

When the vectors are crossed, each pair of orthogonal components (like a_x times b_y) casts a vote for where the orthogonal vector should point. 6 components, 6 votes, and their total is the cross product. (Similar to the gradient, where each axis casts a vote for the direction of greatest increase.)

• xy => z and yx => -z (assume vec(a) is first, so xy means a_x b_y)
• yz => x and zy => -x
• zx => y and xz => -y

xy and yx fight it out in the z direction. If those terms are equal, such as in (2, 1, 0) times (2, 1, 1), there is no cross product component in the z direction (2 – 2 = 0).

The final combination is:

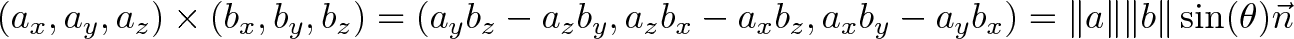
where vec(n) is the unit vector normal to vec(a) and vec(b).

Don’t let this scare you:

• There’s 6 terms, 3 positive and 3 negative
• Two dimensions vote on the third (so the z term must only have y and xcomponents)
• The positive/negative order is based on the xyzxyz pattern

If you like, there is an algebraic proof, that the formula is both orthogonal and of size |a| |b| sin(theta), but I like the “proportional voting” intuition.

Example Time

Again, we should do simple cross products in our head:

Why? We crossed the x and y axes, giving us z (or vec(i) times vec(j) = vec(k), using those unit vectors). Crossing the other way gives -vec(k).

Here’s how I walk through more complex examples:

• Let’s do the last term, the z-component. That’s (1)(5) minus (4)(2), or 5 – 8 = -3. I did z first because it uses x and y, the first two terms. Try seeing (1)(5) as “forward” as you scan from the first vector to the second, and (4)(2) as backwards as you move from the second vector to the first.
• Now the y component: (3)(4) – (6)(1) = 12 – 6 = 6
• Now the x component: (2)(6) – (5)(3) = 12 – 15 = -3

So, the total is (-3, 6, -3) which we can verify with Wolfram Alpha.